Terminología de Redes

Terminología de Redes by on Scribd

PROBLEMA DEL AGENTE VIAJERO

En el Problema del Agente Viajero - TSP (Travelling Salesman Problem), el objetivo es encontrar un recorrido completo que conecte todos los nodos de una red, visitándolos tan solo una vez y volviendo al punto de partida, y que además minimice la distancia total de la ruta, o el tiempo total del recorrido.

Este tipo de problemas tiene gran aplicación en el ámbito de la logística y distribución, así como en la programación de curvas de producción.

El problema del agente viajero tiene una variación importante, y esta depende de que las distancias entre un nodo y otro sean simétricas o no, es decir, que la distancia entre A y B sea igual a la distancia entre B y A, puesto que en la práctica es muy poco probable que así sea. 

La cantidad de rutas posibles en una red está determinada por la ecuación:

(n-1)!

Es decir que en una red de 5 nodos la cantidad de rutas probables es igual a (5-1)! = 24, y a medida que el número de nodos aumente la cantidad de rutas posibles crece factorialmente. En el caso de que el problema sea simétrico la cantidad de rutas posibles se reduce a la mitad, es decir:

( (n-1)! ) / 2

Lo cual significa un ahorro significativo en el tiempo de procesamiento de rutas de gran tamaño.

Los Mapas de Karnaugh

     

Los Mapas de Karnaugh son una herramienta muy utilizada para la simplificación de circuitos lógicos. Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más económica posible se utiliza este método.
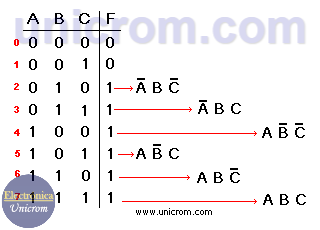
Ejemplo: Se tiene la siguiente tabla de verdad para tres variables. Se desarrolla la función lógica basada en ella. (primera forma canónica). Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a “1”. Si A en la tabla de verdad es “0” se pone A, si B = “1” se pone B, Si C = “0” se pone C, etc.

Reglas de la suma y el producto

1:Si una primera tarea puede realizarse de "m" formas mientras que una tarea puede realizarse de "n" formas y no es posible realizar ambas tareas de manera simultanea, entonces para llevar a cabo cualquiera de ellas puede utilizarse cualquiera de ellas.

2:Si un procedimiento se puede descomponer en las etapas primera y segunda y si existen "m" resultados posibles de la primera etapa, para cada uno de estos resultados existen "n" resultados posibles para la segunda etapa, entonces el procedimiento total que se puede realizar en el orden dado.

Principios fundamentales del conteo

*La enumeración o conteo puede parecer un proceso obvio que u  estudiante aprende a estudiar aritmética por primera vez. Pero luego según parece se presta poca atención en lo que se refiere a un desarrollo más amplio del conteo con forme al estudiante pasa áreas mas difícil de las matemáticas, como el álgebra, geometría, trigonometría y el calculo. En consecuencia deberá servir como advertencia acerca del conteo.

*La enumeración no termina con la aritmética:
también en aplicaciones en áreas como la teoría de códigos como la contabilidad y estadísticas.

Actividades de permutaciones

1:¿Cuantas palabras se pueden formar de 4 letras con la palabra AXEL? 

Escriba el listado de las palabras que se pueden formar.

P4 = 4!                       A          X          E            L
P4 = 4*3*2*1                     axel       xale       exal       lexa
P4 = 24                    alxe       xael       exla       leax
                                aelx       xeal       elax       laxe
                                alex       xela       elxa       laex
                                axle       xlea       eaxl       lxea
                                aexl       xlae       ealx       lxae

2:¿Cuantas palabras diferentes de 5 letras se pueden formar con la palabra libro?

P5 = 5!
P5 = 5*4*3*2*1
P5 = 120 Palabras

3:¿Cuantas palabras diferentes de 6 letras se pueden formar con la palabra tratar?

PRtra = 6!                                                    PRtra = 720
       2! 2! 2!                                                               8

PRtra = 6*5*4*3*2*1                                                           PRtra = 90
          2*1   2*1    2*1


4:¿Cuantas palabras de 10 letras se pueden formar usando la palabra termometro?

P10222 = 10!
       2! 2! 2! 2! 2!

P10222 = 10*9*8*7*6*5*4*3*2*1
            2*1    2*1     2*1      2*1      2*1

P10222 = 1,814,400
                    16

P10222 = 113,400

PERMUTACIONES CIRCULARES

*Se utiliza cuando los elementos se van a ordenar en circulo, por ejemplo los comenzales en una mesa de modo que el primer elemento que se sitúa en la mesa, determina el principio y el fin de la lista.

La formula es:

PCn*1 = n!

1:¿De cuantas formas distintas pueden sentarse 8 personas al rededor de una mesa redonda?

PC8-1 = 7!

PC7   = 7*6*5*4*3*2*1

PC7  = 5,040 Formas de sentarse en la mesa

PERMUTACIONES CON REPETICION

*Se llama permutaciones con repeticion a los diferentes grupos de elementos que se forman usando "n" elementos donde el primer elemento se repite n veces, el segundo tambien se repite n veces y asi consecutivamente hasta llegar al final de la lista. Estas agrupaciones deben seguir las siguientes reglas:

           1:Entran todos los elementos.
           2:Si importa el orden.
           3:Si se repiten los elementos.

*La formula para realizar el calculo de las permutaciones con repeticion es la siguiente:

PRnabc = Pn

                 a!b!c!

1:Con las cifras 2,2,2,3,3,3,3,4 y 4 ¿Cuantos numeros de nueve cifras se pueden formar? n=9, a=3, b=4, c=2

PR93,4,2 = P9!

            3! 4! 2!

PR93,4,2 = 9*8*7*6*5*4*3*2*1

              3*2*1   4*3*2*1    2*1

PR93,4,2 = 362,880

               6*24*2

PR93,4,2 = 362,880

                   288

PR93,4,2 = 1260  Numeros de nueve cifras o permutaciones

PERMUTACIONES

1. Son de n elementos a los diferentes grupos que se pueden formar con esos elementos siguiendo las siguientes reglas:

• Entran todos los elementos
• Si importa el orden 
• No se repiten los elementos

Si el ejercicio que se plantea sigue esas tres reglas, la formula a aplicar es:

Pn=n!

Donde "n" es el numero de elementos que vana participar en las agrupaciones.

Ejercicios

1: ¿Cuantos numeros de 3 cifras diferentes se pueden formar con los digitos 1,2 y 3?

Pn=3!                     P3=3!                                       123

                              P3=3*2*1=6                             132

                                                                                213

                                                                                231

                                                                                312

                                                                                321

2:¿Cuantos grupos diferentes de 3 vocales se pueden formar sin que se repitan los elementos usando las siguientes vocales?

P3=3!                  P3=3*2*1                                  A,E,O

                                         P3=6                                                               A,O,E

                                                                              E,A,O

                                                                              E,O,A

                                                                              O,A,E

                                                                              O,E,A

3:¿Cuantos grupos de 4 elementos se pueden formar con los digitos si no se repiten los elementos?

P4=4!                                3579             3597

P4=4*3*2*1                     3759             3795             3

P4=24                               3957             3975

                                         5379             5397

                                         5739             5793              5

                                         5937             5973

                                         7359             7395

                                         7539             7593              7

                                         7935             7953

                                         9357             9375

                                         9537             9573              9

                                         9735             9753

 4:Antiguamente los barcos se comunicaban entre si utilizando banderas de diferentes colores colocandolas de manera ordenada en diferenes posiciones. ¿Cuantos mensajes distintos se podran enviar con las banderas en los colores azul, rojo, verde y negro? Indique cuantos mensajes serian si se le añade otra bandera cafe.

-En este caso no deberan mostrarselas agrupaciones-

P4=4!                                                P5=5!

P4=4*3*2*1                                     P5=5*4*3*2*1

P4=24 mensajes                               P5=120 mensajes

relacion entre teoria de conjuntos logica matematica y algebra booleana

 Entre logica matematica y teoria de conjuntos comparten leyes logicas tanto para conjuntos como para logica proposicional. El álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional.En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico.

Teoria de subconjuntos

    1:Conjunto de elementos que tienen las mismas características y que está incluido dentro de otro conjunto más 
    2:Un conjunto A es subconjunto de otro B si todos los elementos del primer conjunto son también elementos del segundo conjunto. Esto es;

A⊂B ⇔ ∀x∈A,x∈B 

Ejemplos.

El «conjunto de todos los hombres» es un subconjunto del «conjunto de todas las personas».

{1, 3} ⊆ {1, 2, 3, 4}

{2, 4, 6, ...} ⊆ {1, 2, 3, ..} = N ( {Números pares} ⊆ {Números naturales} )

3:

Diagrama de venn

1: Los diagramas de Venn son esquemas usados en la teoría de conjuntos, tema de interés en matemáticas, lógica de clases y razonamiento diagramático. Estos diagramas muestran colecciones (conjuntos) de cosas (elementos) por medio de líneas cerradas. La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.

Los diagramas de Venn fueron ideados hacia 1880 por John Venn.

2:Un diagrama de Venn usa círculos que se superponen u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos. A menudo, se utilizan para organizar cosas de forma gráfica, destacando en qué se parecen y difieren los elementos.

Teoria de conjuntos

CONJUNTOS
1: Es una colección de elementos con características similares considerada en sí misma como un objeto. Los elementos de unconjunto, pueden ser las siguientes: personas, números, colores, letras, figuras, etc.
2: Es un enunciando una propiedad que permita seleccionar de un conjunto ya formado, aquellos que verifiquen dicha propiedad. Por ejemplo, dentro del conjunto de los números podemos seleccionar el conjunto B de los números pares, en este caso se emplea una letra, por lo general x, para representar un elemento cualquiera y se escribe:

B = { x / x es par} lo que se lee: "B es el conjunto de los números x tales que x es par". Esta forma de definir un conjunto de llama por comprensión. 3: Es lo que está unido, contiguo o incorporado a otra cosa, o que se encuentra mezclado, combinado o aliado con otra cosa diversa. Un conjunto, por lo tanto, es un agregado de varias cosas o personas.

Tiorres de hanoi

TORRES DE HANOI

¿QUE ES?
Las Torres de Hanói es un rompecabezas o juego matemático inventado en 1883 por el matemático francés Édouard Lucas.¹​ Este juego de mesa individual consiste en un número de discos perforados de radio creciente que se apilan insertándose en uno de los tres postes fijados a un tablero. El objetivo del juego es trasladar la pila a otro de los postes siguiendo ciertas reglas. El problema es muy conocido en la ciencia de la computación y aparece en muchos libros de texto como introducción a la teoría de algoritmos.
¿COMO SE RESUELVE?
La fórmula para encontrar el número de movimientos necesarios para transferir n discos desde un poste a otro es: 2ⁿ - 1

El juego, en su forma más tradicional, consiste en tres postes verticales. En uno de los postes se apila un número indeterminado de discos perforados por su centro (elaborados de madera), que determinará la complejidad de la solución. Por regla general se consideran siete discos. Los discos se apilan sobre uno de los postes en tamaño decreciente de abajo a arriba. No hay dos discos iguales, y todos ellos están apilados de mayor a menor radio -desde la base del poste hacia arriba- en uno de los postes, quedando los otros dos postes vacíos. El juego consiste en pasar todos los discos desde el poste ocupado (es decir, el que posee la torre) a uno de los otros postes vacíos. Para realizar este objetivo, es necesario seguir tres simples reglas:

1.           Solo se puede mover un disco cada vez y para mover otro los demás tienen que estar en postes.

2.           Un disco de mayor tamaño no puede estar sobre uno más pequeño que él mismo.

3.           Solo se puede desplazar el disco que se encuentre arriba en cada poste.

Existen diversas formas de llegar a la solución final, todas ellas siguiendo estrategias diversas.

sucecion de fibonacci

La sucesión de Fibonacci, en ocasiones también conocida como secuencia de Fibonacci o incorrectamente como serie de Fibonacci, es en sí una sucesión matemática infinita. Consta de una serie de números naturales que se suman de a 2, a partir de 0 y 1. Básicamente, la sucesión de Fibonacci se realiza sumando siempre los últimos 2 números (Todos los números presentes en la sucesión se llaman números de Fibonacci).

¿Como es?

La sucesión de Fibonacci es la sucesión de números:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

Cada número se calcula sumando los dos anteriores a él.

• El 2 se calcula sumando (1+1)
• Análogamente, el 3 es sólo (1+2),
• Y el 5 es (2+3),
• ¡y sigue!

Ejemplo: el siguiente número en la sucesión de arriba sería (21+34) = 55

¡Así de simple!

Aquí tienes una lista más larga:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...

EJEMPLO:

Triangulo Pascal

triangulo de pascal

¿Que es?
El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico Se empieza con un 1 en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima. Se supone que los lugares fuera del triángulo contienen ceros, de forma que los bordes del triángulo están formados por unos. Aquí sólo se ve una parte; el triángulo continúa por debajo y es infinito.
'¿como se hace?

Cada linea se construye a partir de la anterior.

Con excepción de los números 1, que siempre están en los extremos, cada número es igual a la suma de los dos números que tiene por encima.

aplicaciones para un triangulo de pascal

Coeficientes binomiales

Los números en la línea n del Triángulo de Pascal enlistan los coeficientes de la expansión de (a + b)^n.

Combinaciones

Las combinaciones son una operación básica en Combinatoria, la rama de la matemática que involucra contar grupos de elementos discretos. Por ejemplo, el número de manos posibles de cinco cartas de una baraja de 52 es 52C5

Probabilidad

En una serie de n resultados binomiales, como tener n niños, el número de resultados en el que uno de los eventos de los binomios ocurra k veces, es igual a la entrada k-ésima entrada en la línea n del triángulo de Pascal.

Series de números

En una serie de n resultados binomiales, como tener n niños, el número de resultados en el que uno de los eventos de los binomios ocurra k veces, es igual a la entrada k-ésima entrada en la línea n del triángulo de Pascal.

Caracteristicas de las matematicas discretas

• Los procesos de las matemáticas discretas son contables.
• Las matemáticas discretas corresponden a un área de la matemática que se encarga de estudiar el conjunto de los números naturales, es decir, el conjunto de números finitos e infinitos contables donde los elementos pueden ser contados por separado.
• A los conjuntos ya mencionados se les conoce como grafos o expresiones lógicas y son usados en diferentes campos de la ciencia principalmente en la informática o computación.
• Se encarga del estudio de os conceptos como la continuidad y el cambio continuo.
• Solo son computables las funciones de conjuntos numerables.

¿Que son las matematicas discretas?

1:Las matemáticas discretas son un área de las matemáticas encargadas del estudio de los conjuntos discretos: finitos o infinitos numerables.

En oposición a las matemáticas continuas, que se encargan del estudio de conceptos como la continuidad y el cambio continuo, las matemáticas discretas estudian estructuras cuyos elementos pueden contarse uno por uno separadamente. Es decir, los procesos en matemáticas discretas son contables, como por ejemplo, los números enteros, grafos y sentencias de lógica. Son fundamentales para la ciencia de la computación, porque solo son computables las funciones de conjuntos numerables.

https://es.wikipedia.org/wiki/Matem%C3%A1ticas_discretas

2:Las matemáticas discretas corresponden a un área de la matemática que se encarga de estudiar el conjunto de los números naturales; es decir, el conjunto de números finitos e infinitos contables donde los elementos pueden ser contados por separado, uno por uno. A esos conjuntos se les conoce como conjuntos discretos; un ejemplo de estos conjuntos son los números enteros, los grafos o expresiones lógicas, y son aplicados en diferentes campos de la ciencia, principalmente en la informática o computación.

https://www.lifeder.com/matematicas-discretas/

3:Se encarga del estudio de conjuntos infinitos, la matemática discreta estudia estructuras cuyos elementos pueden contarse uno por uno separadamente. Es decir, los procesos en matemática discreta son finitos y contables. Las matemáticas discretas, a diferencia del Cálculo infinitesimal, estudia procesos con conjuntos contables o numerables, ya sean finitos o infinitos.

https://www.ecured.cu/Matem%C3%A1tica_Discreta

4:Las matemáticas discretas son un área de las matemáticas encargadas del estudio de los conjuntos discretos: finitos o infinitos numerables.

En oposición a las matemáticas continuas, que se encargan del estudio de conceptos como la continuidad y el cambio continuo, la matemáticas discretas estudian estructuras cuyos elementos pueden contarse uno por uno separadamente. Es decir, los procesos en matemáticas discretas son contables, como por ejemplo, los números enteros, grafos y sentencias de lógica.

https://matediscretasjoaquin.webnode.es/trabajos/unidad-1-sistemas-de-numeracion-/tarea-1-definicion-propia-de-matematicas-discretas/

5:Las matemáticas discretas son un área de las matemáticas encargadas del estudio de los conjuntos discretos: finitos o infinitos numerables.

En oposición a las matemáticas continuas que se encarga del estudio de conceptos como la continuidad y el cambio continuo, las matemáticas discretas estudian estructuras cuyos elementos pueden contarse uno por uno separadamente como enteros, grafos y sentencias de lógica.

https://sites.google.com/site/mdisc11211254/unidad-1-sistemas-numericos/00-definicion-de-matematicas-discretas

PREGUNTAS

1:¿Que son las matemáticas discretas? son un área de las matemáticas encargadas del estudio de los conjuntos discretos: finitos o infinitos numerables.

2:¿Como son los procesos en las matemáticas discretas? Son como por ejemplo, los números enteros, grafos y sentencias de lógica. Son fundamentales para la ciencia de la computación, porque solo son computables las funciones de conjuntos numerables.

3:¿A que area de las matematicas corresponden? a un área de la matemática que se encarga de estudiar el conjunto de los números naturales; es decir, el conjunto de números finitos e infinitos 

4:¿Como se les dice a los conjuntos  de las matematicas? conjuntos discretos; un ejemplo de estos conjuntos son los números enteros, los grafos o expresiones lógicas, y son aplicados en diferentes campos de la ciencia, principalmente en la informática o computación.

5:¿De que estudio se encargan las matematicas? de conjuntos infinitos, la matemática discreta estudia estructuras cuyos elementos pueden contarse uno por uno separadamente.

6:¿Cual es la diferencia de las matematicas discretas y el calculo infinitesimal?  las matematicas disctretas estudia procesos con conjuntos contables o numerables, ya sean finitos o infinitos.

7:¿  

8:

9:

10: